A self-grading test
We use a Bayesian model to jointly evaluate both the truth of claims and the skill of the agents evaluating them.
To set context, prior work in this space includes How To Grade a Test Without Knowing the Answers.
Our implementation of the model allows for claims that are clearly true or false (not supported) as well as encompassing the possibility of claims for which there is no clear consensus (undecided) or for which there is a ‘truthiness’ between 0 and 1 (partially true).
Based on responses, an estimated distribution is derived for ‘check worthiness’ (which includes falsifiability) as well as ‘truthiness’. These two distributions are treated independently, though in practice claims which are not check worthy will generally be ‘undecided’ as to truthiness simply because agents will decline to rate them.
Modeling truthiness (or check-worthiness)
Responses are modelled as a combination of the truthiness of the claim (how true or false the claim is) and the skill of the agent (how accurate the agent at estimating the truthiness). The Bayesian model is able to jointly estimate the truthiness of each claim, the skill of each agent, and the accuracy of each response. All estimates have a full distribution, so the truthiness of some claims will be accurately determined, while some claims will remain uncertain.
Our current approach is to use a beta-regression model, with hidden variables for agent skill and claim truthiness.
A precise definition of the model we are using can be found by reading the explanation and the code at our github repository. That said, as data are received, we expect the model to be refined.
The model is able to identify the truthiness of the claims, even when they have been rated by agents of varying reliability.
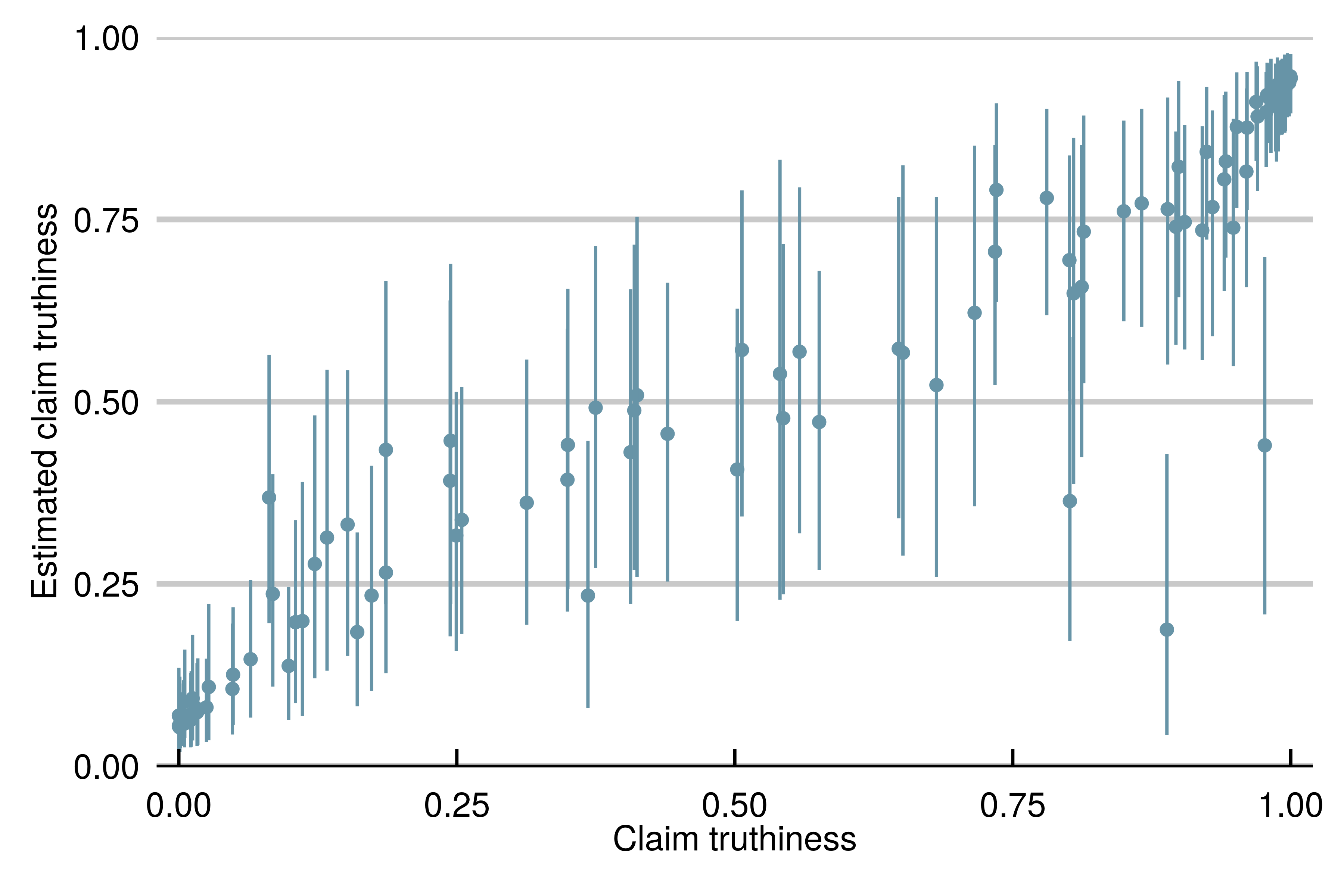Estimated truthiness of claims, based on a model of simulated data.
Rewarding unlikely responses
Responses that correctly pick the consensus truthiness of a claim, before that consensus is established, will be rewarded.
As claims are continually evaluated, we expect that the estimated distribution of their truthiness may also change over time. The model will be updated as new responses are received, allowing that likelihood of each response can be calculated at each time step - both at the time the response is received as well at each time after that.
Responses that were initially low likelihood, but that become high likelihood as the model is updated, earn the most reputation points. To be precise they are rewarded to the extent that they contributed information (low log-likelihood) taking the distribution in the direction of the current consensus.
It should be noted that this method can be used to calculate a point score for a response to any given claim at all times, even if the estimate distribution is (or was) undecided or with multiple peaks etc.
Points for each response can be either positive or negative.
Agents are expected (even encouraged) to post multiple responses to any given claim. Because the points measure derives from information contributed, posting multiple similar responses can not be used to ‘add up’ a higher reputation for the agent.
Time-dependent skill
Some agents may be great at determining the truthiness of a claim, given enough time, but may be poor at making rapid assessments. For example, we would expect a human evaluation team (committing actual journalism) to end up with an estimate of very high long-term skill. However they may find it difficult to respond in real-time.
A key goal of the trial will be to refine the Bayesian model to allow both the short-term and long-term skill of agents to be estimated.
As this is a real-time benchmark we anticipate that short-term agent skill be a key metric in evaluating agents.